|
|
|
Соотношение между градусной и радианной мерами угла
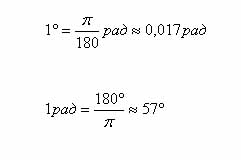
Определения:
Тригонометрические функции острых углов можно определить как отношение длин сторон прямоугольного треугольника.
Синус:
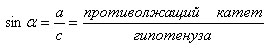
Косинус:
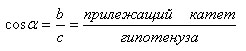
Тангенс:
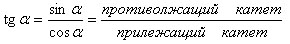
Котангенс:
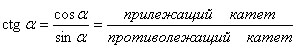
Синус и косинус угла определены для любого угла α. Тангенс определен для всех значений угла α, кроме α = π/2
+ πn (a = 90º + 180º * n), n = 0, +/- 1, +/- 2,... .
Котангенс определен для всех значений угла α, кроме α = πn (α = 180º * n), n = 0, +/- 1, +/- 2, ...
Секанс:
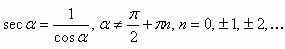
Косеканс:
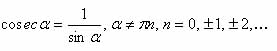
Периодичность
Функции sin α , cos α, sec α и cosec α имеют период 2π, а функции tg α и ctg α
- период π:
sin(α + 2πn) = sin α; cosec(α + 2πn) = cosec α;
cos(α + 2πn) = cos α; sec α + 2πn) = sec α;
tg (α + πn) = tgα;
ctg (α + πn) = ctg α; n = 0, +/- 1, +/- 2,... .
Формулы приведения
Вычисление значений тригонометрических функций любого угла сводится к вычислению значений
тригонометрических функций острого угла по следующим правилам:

Некоторые значения тригонометрических функций
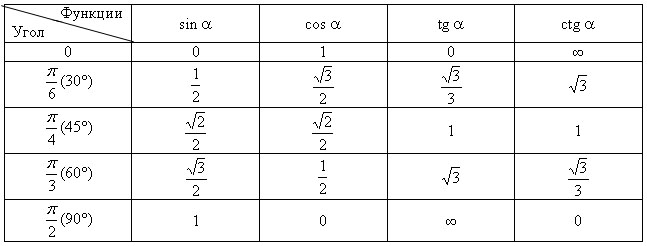
Основные тригонометрические тождества
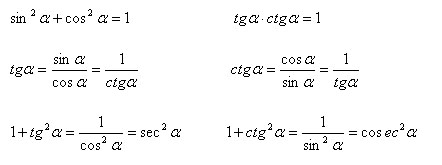
Четность и нечетность тригонометрических функций
Функция F(x) называется четной, если F(-x)=F(x).
Функция F(x) называется нечетной, если F(-x)=-F(x).
Функция F(x) называется ни четной, ни нечетной во всех остальных случаях.
sin α, tg &alpha, ctg &alpha и cosec &alpha - функции нечетные.
sin(- α) = - sin α
tg(- α) = - tg α;
ctg(- α) = - ctg α;
cosec(- α) = - cosec α.
cos α и sec α - функции четные.
cos(- α) = cos α;
sec(- α) = sec α.
Тригонометрические функции суммы и разности углов
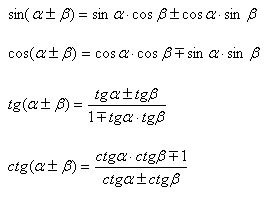
Выражение sinα, cosα, tgα через tg(α/2)
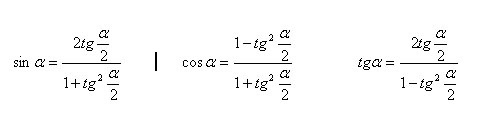
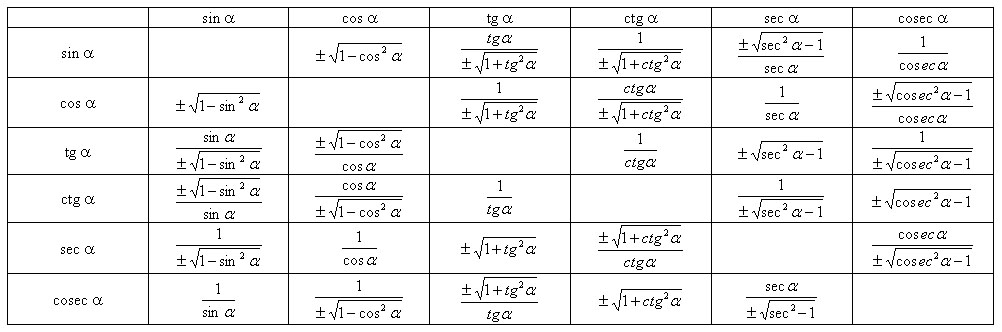
Выражение одних тригонометрических функций через другие
Тригонометрические функции двойных, тройных и половинных углов

В формулах половинного угла знаки перед радикалами берутся в зависимости от знака тригонометрической функции,
стоящей в левой части равенства.
Каждая из формул для тангенса и котангенса справедлива только при условии,
что все входящие в нее значения функций существуют.
Преобразование суммы (разности) тригонометрических функций в произведение (преобразование
тригонометрических выражений к виду, удобному для логарифмирования).
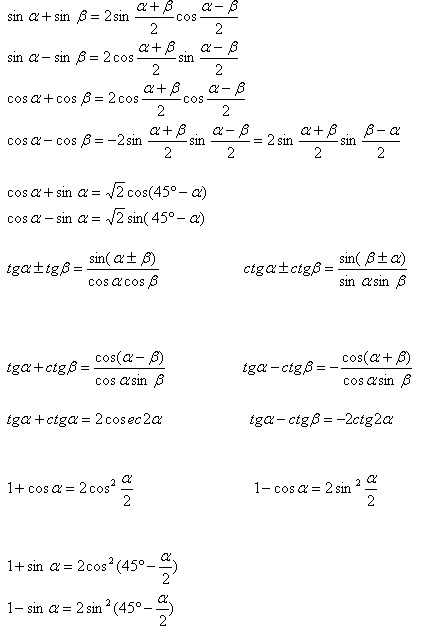
Преобразование произведения тригонометрических функций в сумму.
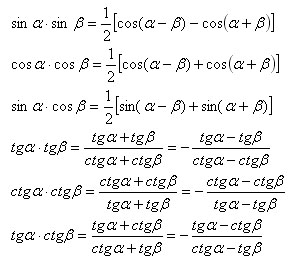
Правая и левая части каждой формулы, в которую входят тангенсы и (или) котангенсы, должны существовать одновременно.
Простейшие соотношения между обратными тригонометрическими функциями.
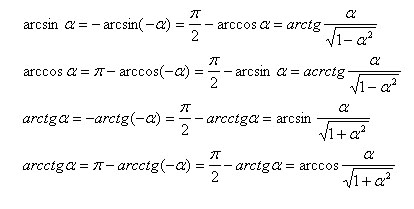
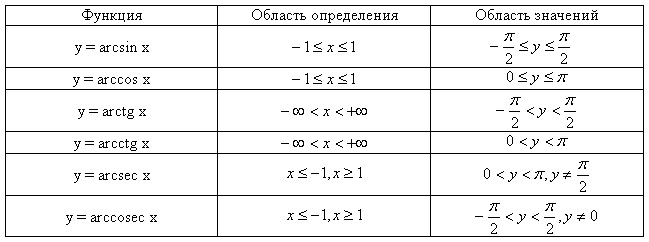
Решение тригонометрических уравнений.
cos(x)= a
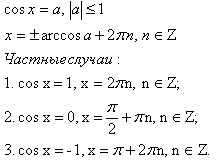
sin(x)= a
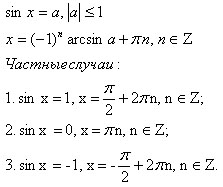
tg(x)= a
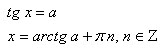
ctg(x)= a
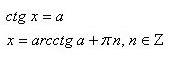
|
| |
|
|