|
|
|
Пример исследования функции для построения эскиза графика.
Исследуем функцию f(X)=1/(x2+1) и согласно полученным результатам нарисуем эскиз ее графика.
Сначала найдем область определения функции. Так как знаменатель дроби не обратится в нуль ни при каких
значениях x, функция определена на всей числовой прямой - x может принимать любые значения. Заметим, что
функция f(x) четная, так как f(-x)=1/((-x)2+1)=1/(x2+1)=f(x). Так как функция четная,
то достаточно ее исследовать и построить эских графика только для положительных х, а затем отразить эскиз
относительно оси ординат. Теперь найдем точки пересечения графика функции с координатными осями. С осью ординат
график пересекается в точке (0; f(0)). Для нашей функции это точка (0;1), так как f(0)=1. Для того, чтобы
найти точки пересечения с осью абсцисс, надо решить уравнение f(x)=0. Уравнение 1/(x2+1)=0 не
имеет действительных корней, значит график f(x) не пересекает ось абсцисс. Из этого можно сделать вывод,
что график функции либо весь располагается над осью абсцисс (функция всюду положительная), либо весь под ней
(функция всюду отрицательна). Очевидно, что дробь 1/(x2+1) при любых х принимает положительные
значения, значит график нашей функции весь располагается над осью абсцисс.
При построении графика функции очень полезно иметь информацию о промежутках возрастания и убывания функции.
Используя определения возрастающих и убывающих функций, можно определить, что f(x)
возрастает на промежутке (-; 0] и убывает на промежутке [0; ). Таким образом, в точке x=0 возрастание
функции сменяется на убывание. f(0)=1.
Так же заметим, что при неограниченном увеличении аргумента знаменатель f(x) неограниченно увеличивается,
следовательно значение функции спадает до нуля (неограниченно приближается к нулю). Исходя из четности функции
можно сказать, что функция ведет себя точно так же и при неограниченно уменьшении аргумента.
Исходя из полученной информации мы можем нарисовать эскиз графика функции, он представлен на рисунке ниже.
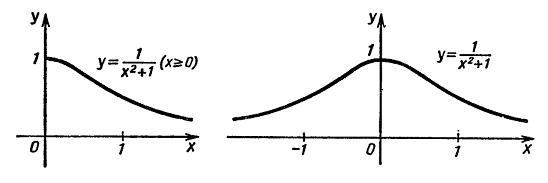
Далее рассмотрим общую схему исследования функций.
|
| |
|
|