|
|
|
Уравнение четвертой степени общего вида
|
|
Уравнение четвертой степени общего вида
ax4 + bx3 + cx2 + dx + e = 0. - Уравнение четвертой степени общего вида.
1. Сокращение до неполного уравнения
Уравнение четвертой степени в общем сокращается до неполного уравнения
y4 + py2 + qy + r = 0
при помощи замены переменных
x = y - b/4a
2. Решение Декарта - Эйлера
Корни неполного уравнения четвертой степени определяются формулами:
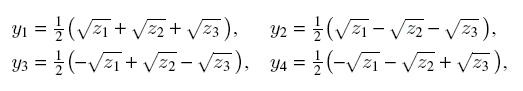
где z1, z2, z3 это корни кубического уравнения
z3 + 2pz2 + (p2 - 4r) - q2 = 0,
которое называется резольвентой исходного уравнения. Знаки корней в ней выбираются таким образом,
чтобы выполнялось равенство:
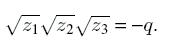
Корни неполного исходного уравнения определяются корнями кубической резольвенты
согласно таблице:
Связь между корнями неполного уравнения четвертой степени и корнями резольвенты
| Кубическая резольвента | Уравнение четвертой степени |
| Все корни действительные и положительные (*) | Четыре действительных корня |
| Все корни действительные, они положительный и два отрицательных (*) | Две пары комплексно сопряженных корней |
| Один корень положительный, два комплексно-сопряженные | Два действительных и два комплексно-сопряженных корня |
(*) - по теореме Виета, произведение корней z1, z2, z3 = q2
3. Решение Феррари
Предположим, z0 - один из корней вспомогательного кубического уравнения.
z3 + 2pz2 + (p2 - 4r) - q2 = 0,
Тогда четрые корня неполного уравнения четвертой степени находятся при помощи решения двух
квадратных уравнений
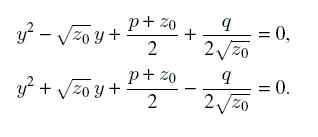
|
| |
|
|